(Note for international readers: English version will follow but for now you can use google translate)

Već nam je dugo poznato da WRF model generalno daje niže temperature nad snijegom prekrivenim područjem. Zavisno o upotrijebljenim shemama, karakteristikama regije te aktualnih meteoroloških uvjeta, odstupanja su manja ili veća i manifestiraju se u drugačijem dijelu dana. Problem je čini se generalnije prirode i nije vezan samo za MeteoAdriatic model. Tome svjedoče objavljeni radovi u znanstvenim časopisima (Tomasi et al., 2017; Varga et al., 2020; Meng et al., 2018), materijali s radionica (Mass & Ovens, 2013), te objave na službenom WRF/MPAS-A forumu (WRF/MPASa, 2020; WRF/MPASb, 2019). Većina autora smatra da je razlog negativnog biasa prevelik albedo površine (snijega), zbog čega ista ne prima dovoljnu količinu sunčevog zračenja tokom dana i stoga ostaje hladnija od realne temperature. I premda u tome može biti dosta istine, mi smo u MeteoAdriatic-u zaključili da to nije dovoljno nakon što smo implementirali niz sugeriranih korekcija u Tomasi et al., 2017 te Meng et al., 2018. Posebno stoga jer se pokazuje da negativna greška temperature jako raste tokom vedrih noći u nizinskim krajevima prekrivenim snijegom, te smo zaključili da problematika nije vezana isključivo za albedo snijega. Krenuli smo stoga istraživati i u drugom smjeru; to ne znači da je naš pristup nužno ispravan niti da smo otkrili stvaran razlog ovih odstupanja temperature, ali ono što smo pronašli i modificirali nama za sad funkcionira. Ispod je kratko opisana metedologija i rezultat.

Većina referenci upućuje da se srž problema krije u LSM shemi, točnije NOAH i NOAH-MP modelu. Stoga smo odlučili potražiti moguće razloge tamo. Pokazalo se je pritom da korištena NOAH-MP shema iz nekog razloga postavlja koeficijent emisivnosti snijega svugdje = 1. To naime fizikalno nije ispravno; samo tzv. crno tijelo (engl. black body) može imati ε=1. Koeficijent emisivnosti govori o sposobnosti materije da zrači toplinsku energiju u prostor i može iznositi od 0 (ako ne zrači ništa) pa do 1 (ako nijedan proces ne zapriječava zračenje energije s površine tijela u prostor). Realistične vrijednosti emisivnosti tla se kreću od 0,9 do 0,98 (Evett et al., 2011), dok snijeg ima emisivnost oko 0,97 (Kondo et al., 1986) ali prema nekim izvorima može imati i manje (Rees, 1993).

Ovdje dolazimo do NOAH-MP koda koji računa emisivnost snijega (ver. 4.2.2, datoteka phys/module_sf_noahmplsm.F, linije 1906 i 1908):

EMG = 0.98*(1.-FSNO) + 1.0*FSNO (1)

EMG = parameters%EG(IST)*(1.-FSNO) + 1.0*FSNO (2)

Jednadžba 1 računa emisivnost tla ako je površina zaleđena, a jednadžba 2 ako nije. Pritom parametri u jednadžbi 2 dolaze iz datoteke MPTABLE.TBL (run direktorij) i iznose 0.97 za tlo i 0.98 za vodene površine. FSNO je postotak površine prekriven snijegom (engl. snow fraction), od 0 – nema snijega na tlu u ćeliji modela, do 1 – cijela površina ćelije u modelu je prekrivena snijegom. Brza provjera s FSNO brojkama nam govori da onda kad snijega nema, da je rezultat emisivnosti zaleđene površine, kao i vodenih masa = 0,98, te ostalih površina = 0,97, no ako je ćelija u modelu prekrivena sa snijegom, emisivnost tla će biti = 1 u obje jednadžbe. Mi smatramo da je to pogrešno i da dovodi do pretjeranog noćnog zračenja s tla (kojeg u modelu računa radijacijska shema, temeljem ove emisivnosti i drugih parametara poput naoblake, itd.).

Stoga smo odlučili modificirati ove jednadžbe te umjesto 1.0 staviti 0.97 prema Kondo et al. (1986), no za izraženiji učinak može se staviti niži broj (vidi mjerenja od Rees, 1993):

EMG = 0.98*(1.-FSNO) + 0.97*FSNO (1mod)

EMG = parameters%EG(IST)*(1.-FSNO) + 0.97*FSNO (2mod)

Nakon ovih izmjena, kod je potrebno prekompajlirati. Dodatno na to, prema Evett et al. (2011), emisivnost tla bi trebala u prosjeku biti niža od default vrijednosti u MPTABLE.TBL (0.97). Stoga, u toj datoteci možete sniziti i tu vrijednost, što će dati nižu emisivnost i tla koje nije prekriveno snijegom (čini se, da snižavanje daje realističnije rezultate). Linija 310, run/MPTABLE.TBL:

EG = 0.97, 0.98

Ovdje je prvi broj (0.97) onaj kojeg želite mijenjati, dok se drugi odnosi na emisivnost vodenih površina i čini se da je realan. Što više snizite taj broj, kao i onaj za emisivnost snijega u phys/module_sf_noahmplsm.F, to će rezultirajuća emisivnost podloge u modelu biti niža a time će se gubiti manja količina energije dugovalnim zračenjem, te će tlo ostajati toplije tokom noći što će u konačnici rezultirati višim noćnim prizemnim temperaturama zraka u situacijama kad dominantnu ulogu u njihovom određivanju ima točnost računanja dugovalnog zračenja. Naravno, nakon izmjene MPTABLE.TBL, nije potrebno rekompajlirati model.

Dodatno na to, prema spomenutim referencama, vjerojatno će biti potrebno omogućiti primanje veće količine toplinske energije tokom dana površinama pod snijegom, smanjenjem albeda snijega. Zahvat također možete uraditi u MPTABLE.TBL, linije 337 i 338 (BATS_VIS_NEW, BATS_NIR_NEW, smanjenjem tih vrijednosti, a možete se eksperimentirati dodatno i sa linijama BATS_VIS_AGE, BATS_NIR_AGE, BATS_VIS_DIR, BATS_NIR_DIR … – vidjeti u LSM kodu kakav učinak imaju ti parametri na rezultirajuću vrijednost albeda).

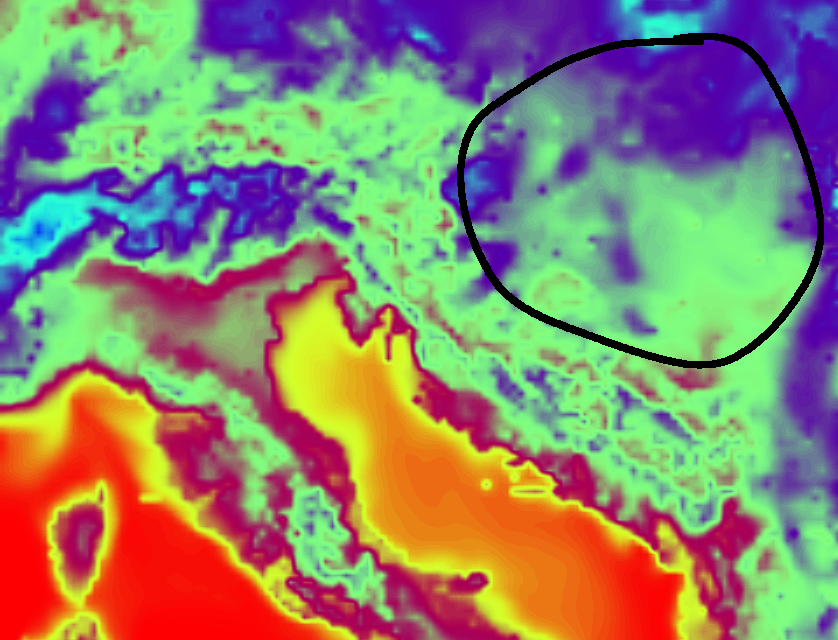
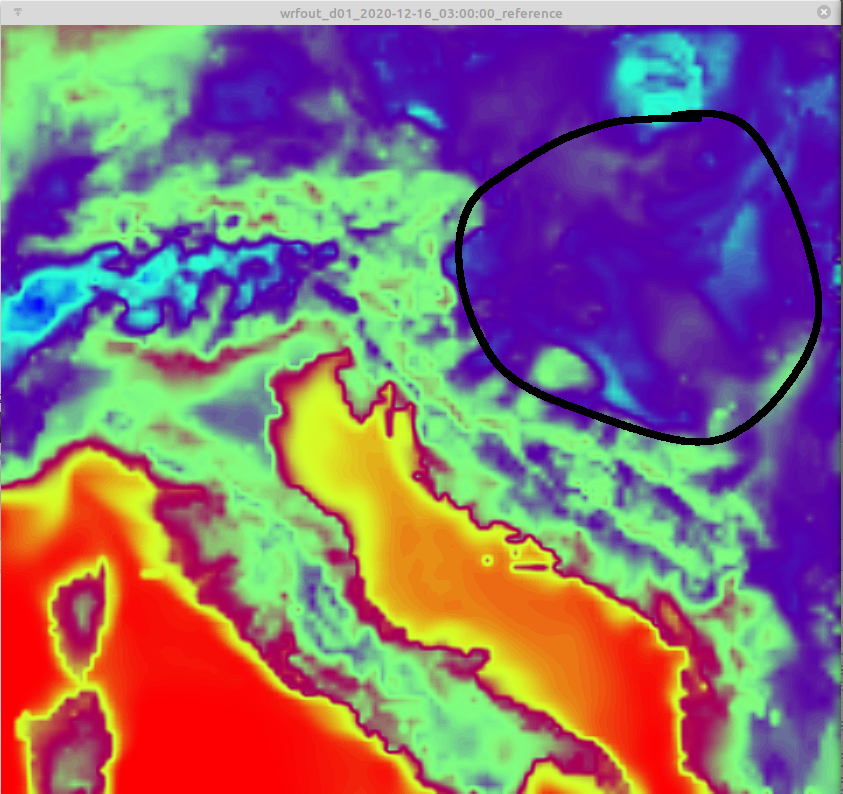
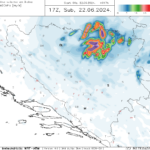
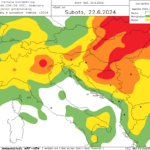
Svi spomenuti zahvati zajedno, daju prilično izražen učinak na neutraliziranje hladnog biasa nad podlogom pod snijegom. Na sljedećem primjeru pokazani su rezultati testne simulacije, pri čemu lijeva slika daje noćne temperature s originalnim kodom i MPTABLE.TBL vrijednostima, dok desna daje rezultate s modificiranim NOAH-MP i MPTABLE.TBL datotekama.

Usporedba simulacije s modificiranim NOAH-MP kodom za emisivnost snijega, te modificiranom emisivnošću tla i albedom snijega u MPTABLE.TBL. Temperature nad podlogom pod snježnim pokrivačem su izraženo više, posebice tamo gdje su one sinoptički određene prvenstveno dugovalnim zračenjem.

Naravno, idealne vrijednosti izmijenjenih parametara u kodu i MPTABLE.TBL datoteci zavisit će od slučaja do slučaja, te nije moguće dati egzaktnu vrijednost koja će dati univerzalno najbolji rezultat.

Reference: